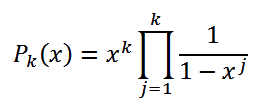Esta entrada es la segunda parte de nuestra participación en la Edición 4.1231 del Carnaval de Matemáticas cuyo anfitrión es Matemáticas Interactivas y Manipulativas.
Estudiamos en la entrada anterior el retículo de los divisores de N. Ahora buscaremos subretículos del mismo.
El retículo de los libres de cuadrados
Lo presentaremos con un ejemplo. Imaginemos todos los divisores de 1800 que son libres de cuadrados, es decir, que sus factores primos están todos elevados a la unidad. Es claro que cualquier divisor de ellos lo será también del radical de de 1800, que es 30 (contiene los mismos factores primos, pero elevados a la unidad). Por tanto, esto nos remite al caso general: es retículo el conjunto de divisores de un número libre de cuadrados (ver entrada anterior).
En el caso de 1800 son estos: {30, 15, 10, 6, 5, 3, 2, 1} Todos presentan los primos 2, 3 o 5 elevados a la unidad. El mayor, 30, es el radical de 1800. Como es libre de cuadrados, sus divisores formarán un retículo.
La imagen te lo explica perfectamente. Cada par de elementos tiene un supremo y un ínfimo. Todo el conjunto posee un máximo, que es 30 y un mínimo 1.
En este retículo todo elemento a posee un complemento a’, formado por los factores primos que no son divisores de a. Es claro que el supremo de a y a’ es 30 y el ínfimo 1. Por tener esta propiedad este retículo es complementado.
Hemos descubierto que en el conjunto de divisores de un número cualquiera, los libres de cuadrados forman un subretículo, que coincide con los divisores del radical de N. Este retículo es complementado.
Por ejemplo, en el número 4900, el subretículo de los libres de cuadrados está formado por el conjunto {70, 35, 14, 10, 7, 5, 2, 1 }
¿Qué ocurre con los que no son libres de cuadrados?
Un divisor no libre de cuadrados admite a su vez otro divisor suyo que sí lo sea. 90 no está libre de cuadrados, pues equivale a 2*32*5, pero admite como divisor el 15 que sí es libre de cuadrados. Es un conjunto que no es sub_semirretículo para la relación de ser divisor. En el caso de 1800 es este: {1800, 900, 600, 450, 360, 300, 225, 200, 180, 150, 120, 100, 90, 75, 72, 60, 50, 45, 40, 36, 25, 24, 20, 18, 12, 9, 8, 4}
Si cambiamos la relación de “ser divisor” por la de “ser múltiplo”, la idea se invierte: Cualquier múltiplo de un divisor no libre de cuadrados tampoco lo será, y lo convierte en un sup_semirretículo para la relación de “ser divisor”. Así que en el conjunto de los divisores no libres de cuadrados todo par de ellos posee un supremo que pertenece al conjunto, pero quizás no exista el ínfimo. Con un ejemplo lo verás: 1800=MCM(450,24) es el supremo de ambos, y está en el conjunto. Sin embargo 6=MCD(450,24) no lo está.
Caso de los pares e impares
Con los divisores pares e impares de un número ocurre algo parecido. Lo resumimos rápidamente:
Los divisores de un número impar han de ser también impares
Los múltiplos de un número par han de ser pares.
Así que si clasificamos los divisores de un número en pares e impares, veremos que ambos conjuntos serán un retículo. Observa el caso de 840:
Pares: {840, 420, 280, 210, 168, 140, 120, 84, 70, 60, 56, 42, 40, 30, 28, 24, 20, 14, 12, 10, 8, 6, 4, 2}
Impares:{105, 35, 21, 15, 7, 5, 3, 1}
En efecto, los impares forman retículo, porque 105 es el mayor divisor impar, (http://hojaynumeros.blogspot.com.es/2012/12/volvemos-visitar-al-mayor-divisor-impar.html) obtenido eliminando del 840 todas las potencias de 2 y quedándonos con todos los factores impares de 840. Por tanto, los demás divisores impares lo serán también de 105, y es fácil ver que forman un sup_semirretículo.
Hacia abajo es mucho más fácil razonarlo: todo divisor de un impar es también impar, lo que nos lleva a que sea un sub_semirretículo, y por tanto, un retículo. Esto es válido para cualquier número que no sea potencia de 2, ya que entonces el conjunto de divisores impares se reduciría a 1.
Los pares también forman retículo. Sólo se pueden considerar si N es par, como es evidente. El MCD de dos pares también será par, con un ínfimo en el 2. El MCM también lo será con mayor razón, con supremo N, que hemos supuesto que es par. También forman retículo.
Si el mayor divisor par propio, o el mayor divisor impar propio son libres de cuadrados, sus retículos correspondientes serán complementados. Un ejemplo de este tipo, el factorial de 5, 120, es libre de cuadrados, luego también lo serán su mayor divisor par 60 y el mayor impar 15, que dan lugar a los retículos {120, 60, 40, 30, 24, 20, 12, 10, 8, 6, 4, 2} y {15, 5, 3, 1} respectivamente.
Te puedes distraer buscando el complemento de cada uno de los elementos, tanto en los subretículos como en el retículo total.
Múltiplos de uno de los factores primos
Considera los divisores de N que son múltiplos de uno de los factores primos. Por ejemplo, en el conjunto de divisores de 3850: {3850, 1925, 770, 550, 385, 350, 275, 175, 154, 110, 77, 70, 55, 50, 35, 25, 22, 14, 11, 10, 7, 5, 2, 1} podemos seleccionar los que son múltiplos de 11: {3850, 1925, 770, 550, 385, 275, 154, 110, 77, 55, 22, 11}. Es un retículo, porque si 11 divide a dos elementos del conjunto, también divide a su MCD, luego éste también pertenece al conjunto. Su MCM también será múltiplo de 11 y divisor de 3850, luego será también elemento del conjunto. Su máximo es el número N, 3850, y el mínimo 11.
¿Qué ocurre con los que no son múltiplos de ese factor primo?
En el ejemplo serían {350, 175, 70, 50, 35, 25, 14, 10, 7, 5, 2, 1}, pero esos son los divisores de 350, que forman retículo (razónalo) y coinciden en número con los del anterior. Es más, podemos establecer una correspondencia biyectiva entre los múltiplos de 11 y los que no lo son:
3850 350
1925 175
770 70
550 50
385 35
275 25
154 14
110 10
77 7
55 5
22 2
11 1
En este diagrama, al que hemos suprimido líneas, se ve bien la correspondencia:
En realidad, estamos ante un isomorfismo de retículos, porque cualquier MCD o MCM del primero, al multiplicar por 11 se convierte en el MCD o MCM en el segundo. Razónalo.
Esto ha sido casual, porque hemos elegido 11, que está elevado a la unidad. Retrocede al caso de pares e impares que estudiamos antes y comprobarás que no se da ese isomorfismo.
¿Se dará siempre que el factor primo esté elevado a la unidad?
Lo vemos:
Si el numero N contiene a p con exponente 1 en su descomposición en factores primos, sus divisores se dividirán en dos subconjuntos, A, los que contienen a p, es decir tienen la forma p*q, y B, los que no lo contienen. Pero si piensas un momento el factor q que hemos usado, recorrerá B mientras p*q recorre A.
En este caso se da un isomorfismo entre los divisores múltiplos de p y los que no lo son. La expresión e este isomorfismo es F(x)=p*x, con x elemento de A y F(x) elemento de B
Así que el caso de 3850 no era una excepción.
Caso en el que el factor primo está elevado a un exponente mayor
Lo intentamos con los múltiplos de 5 en ese mismo ejemplo del 3850:
{3850, 1925, 770, 550, 385, 350, 275, 175, 110, 70, 55, 50, 35, 25, 10, 5}
Y los que no lo son
{154, 77, 70, 22, 14, 11, 7, 2, 1}
Vemos que hay la mitad de elementos, porque 5 está al cuadrado. Si eligiéramos el conjunto de los múltiplos de 25 y el de los de 5 que no lo son de 25 nos resultarían tres conjuntos con el mismo cardinal
No múltiplos de 5: {154, 77, 70, 22, 14, 11, 7, 2, 1}
Múltiplos de 5 pero no de 25: {770, 385, 110, 70, 55, 35, 10, 5}
Múltiplos de 25: {3850, 1925, 550, 350, 275, 175, 50, 25}
Es fácil ver que los tres son retículos isomorfos. Intenta una generalización.
Múltiplos de cualquier divisor dado
¿Formarán también retículo los múltiplos de un divisor dado? Un ejemplo: entre los divisores de 600 seleccionar los que son múltiplos de 15
Todos los divisores de 600 son: {600, 300, 200, 150, 120, 100, 75, 60, 50, 40, 30, 25, 24, 20, 15, 12, 10, 8, 6, 5, 4, 3, 2, 1}
Los que son múltiplos de 15:{600, 300, 150, 120, 75, 60, 30, 15} y los que no lo son
{200, 100, 50, 40, 25, 24, 20, 12, 10, 8, 6, 5, 4, 3, 2, 1}
Es claro que en el primero el MCD y el MCM de dos múltiplos de 15 también lo es. El segundo no es retículo, porque no contiene el MCM(3,5)=15.
Los múltiplos de cualquier divisor de N constituyen un retículo, pero los que no lo son no tienen que serlo.
Este blog es un complemento natural de mi página http://www.hojamat.es. Por ello, se dedicará a los temas numéricos tratados con Hoja de Cálculo y a la estructura y prestaciones de esta. Su nivel será elemental o medio, y su orientación lúdica e investigadora.
sábado, 25 de mayo de 2013
miércoles, 22 de mayo de 2013
Números libres de cuadrados
Documento de Rafael Parra Machío
Otra interesante aportación al proyecto Hojamat de nuestro amigo y colaborador . Define y analiza en él los números libres de cuadrados, con interesante desarrollo de sus propiedades y la aportación de sucesiones inéditas.
Lo puedes descargar desde http://hojamat.es/parra/NumerosLDC.pdf
Insertamos la imagen de una de sus páginas
Otra interesante aportación al proyecto Hojamat de nuestro amigo y colaborador . Define y analiza en él los números libres de cuadrados, con interesante desarrollo de sus propiedades y la aportación de sucesiones inéditas.
Lo puedes descargar desde http://hojamat.es/parra/NumerosLDC.pdf
Insertamos la imagen de una de sus páginas
lunes, 20 de mayo de 2013
Retículos en el conjunto de divisores (1)
Esta entrada y la siguiente participan en la Edición 4.1231 del Carnaval de Matemáticas cuyo anfitrión es Matemáticas Interactivas y Manipulativas.
El conjunto de divisores de un número natural N está ordenado parcialmente mediante la relación de orden a|b (“a divide a b”) que es reflexiva, simétrica y transitiva, pero en la que dos elementos pueden no ser comparables: ni 6 divide a 13 ni 13 a 6. Por ello decimos que se trata de un orden parcial. En cualquier texto o página específica puedes leer más detalles. Con un nivel elemental, en nuestro documento sobre Teoría de la Divisibilidad http://hojamat.es/sindecimales/divisibilidad/teoria/teordivi.pdf
Quizás sepas que el conjunto de los divisores de un número tiene estructura de retículo. Como este blog no va de Álgebra, sólo daremos una noción de este concepto en su variante de orden (existe otra definición algebraica y ambas son equivalentes)
Definimos
Se dice que un conjunto ordenado es filtrante superiormente si para cada par de elementos a y b del mismo existe al menos otro elemento del conjunto que es mayorante de ellos (en nuestra relación de divisibilidad se traduciría como “múltiplo común”). Lo será inferiormente si existe un minorante de ambos (aquí sería un “divisor común”).
El conjunto de los divisores de N está filtrado superior e inferiormente, y además, para cada par de elementos existe un supremo, que es el mayorante mínimo (el mínimo común múltiplo), que representaremos como aÚb y un ínfimo (el máximo común divisor), representado como aÙb.
Por estas dos propiedades recibe el nombre de retículo.
Sería semirretículo si sólo cumpliera una. Investiga en un tratado de Álgebra las propiedades de estas operaciones (conmutativa, asociativa, absorbente, idempotente…). Si sólo se garantiza la existencia de un supremo, el retículo se convertiría en un sup_semirretículo, y sub_semirretículo en el caso del ínfimo.
Un retículo puede ser acotado si existe un máximo E que es mayorante de todos los demás elementos, y un mínimo F que es minorante de todos ellos. Es claro que en nuestro ejemplo N es el máximo E y 1 es el mínimo F. Se cumple que NÙb=b y que 1Úb=b. A los elementos que sólo tienen como minorante F (y distintos de él) les llamaremos átomos, y en nuestro caso son los factores primos de N. Por el contrario, si su único mayorante es E, reciben el nombre de coátomos.
Estos dos elementos E y F nos valen para la siguiente definición: un retículo acotado es complementado si para todo elemento a existe otro a’, su complemento, tal que aÚa’=E y aÙa’=F. Aunque no nos extenderemos en esta dirección, el complemento no tiene que ser único.
Puedes investigar cuándo un retículo se convierte en un álgebra de Boole. No trataremos esto aquí.
Aquí hay que pararse:
El retículo de los divisores de N es complementado si y sólo si N es libre de cuadrados.
En efecto: Si N es libre de cuadrados, todos sus factores primos estarán elevados a la unidad, por lo que cada divisor a se caracterizará tan sólo por su colección de factores primos, y bastará tomar para a’ el número formado por el producto de los primos que no son divisores de a, que cumplirá trivialmente lo exigido. Por ejemplo, entre los divisores de 210 (libre de cuadrados porque 210=2*3*5*7), el complemento de 35 es 14.
Por el contrario, si no es libre de cuadrados, un divisor al menos p se presenta elevado a una potencia con exponente r mayor que 1. Busquemos el complemento q de p (sin elevar a r). En primer lugar deberá cumplir que pÙq=F o expresado mejor en este caso, p y q han de ser coprimos. Entonces q sólo podrá contener factores primos distintos de p. Pero al calcular pÚq el resultado no podrá coincidir con N, ya que el MCM(p, q) contendrá a p elevado a la unidad, mientras que N lo contiene elevado a r>1. Así que ningún candidato a complemento cumple las dos propiedades. Hemos encontrado un contraejemplo que invalida la propiedad.
Este carácter de retículo se suele expresar mediante un diagrama de Hasse, en el que cada dos elementos relacionados se unen mediante una línea, no teniendo en cuenta la propiedad reflexiva y aprovechando la transitiva para eliminar líneas. Aquí tienes el correspondiente a 150:
Se comprende que hay otras formas de ordenarlo y dibujarlo. Es un buen ejercicio identificar el carácter de un número según su diagrama de divisores (potencia de un primo, semiprimo, libre de cuadrados…)
Presentada esquemáticamente la teoría, nos dedicaremos a descubrir algunos retículos y semirretículos que se dan en el conjunto de divisores de N. Todo él completo hemos visto que es un retículo.
Pero eso queda para otro día
El conjunto de divisores de un número natural N está ordenado parcialmente mediante la relación de orden a|b (“a divide a b”) que es reflexiva, simétrica y transitiva, pero en la que dos elementos pueden no ser comparables: ni 6 divide a 13 ni 13 a 6. Por ello decimos que se trata de un orden parcial. En cualquier texto o página específica puedes leer más detalles. Con un nivel elemental, en nuestro documento sobre Teoría de la Divisibilidad http://hojamat.es/sindecimales/divisibilidad/teoria/teordivi.pdf
Quizás sepas que el conjunto de los divisores de un número tiene estructura de retículo. Como este blog no va de Álgebra, sólo daremos una noción de este concepto en su variante de orden (existe otra definición algebraica y ambas son equivalentes)
Definimos
Se dice que un conjunto ordenado es filtrante superiormente si para cada par de elementos a y b del mismo existe al menos otro elemento del conjunto que es mayorante de ellos (en nuestra relación de divisibilidad se traduciría como “múltiplo común”). Lo será inferiormente si existe un minorante de ambos (aquí sería un “divisor común”).
El conjunto de los divisores de N está filtrado superior e inferiormente, y además, para cada par de elementos existe un supremo, que es el mayorante mínimo (el mínimo común múltiplo), que representaremos como aÚb y un ínfimo (el máximo común divisor), representado como aÙb.
Por estas dos propiedades recibe el nombre de retículo.
Sería semirretículo si sólo cumpliera una. Investiga en un tratado de Álgebra las propiedades de estas operaciones (conmutativa, asociativa, absorbente, idempotente…). Si sólo se garantiza la existencia de un supremo, el retículo se convertiría en un sup_semirretículo, y sub_semirretículo en el caso del ínfimo.
Un retículo puede ser acotado si existe un máximo E que es mayorante de todos los demás elementos, y un mínimo F que es minorante de todos ellos. Es claro que en nuestro ejemplo N es el máximo E y 1 es el mínimo F. Se cumple que NÙb=b y que 1Úb=b. A los elementos que sólo tienen como minorante F (y distintos de él) les llamaremos átomos, y en nuestro caso son los factores primos de N. Por el contrario, si su único mayorante es E, reciben el nombre de coátomos.
Estos dos elementos E y F nos valen para la siguiente definición: un retículo acotado es complementado si para todo elemento a existe otro a’, su complemento, tal que aÚa’=E y aÙa’=F. Aunque no nos extenderemos en esta dirección, el complemento no tiene que ser único.
Puedes investigar cuándo un retículo se convierte en un álgebra de Boole. No trataremos esto aquí.
Aquí hay que pararse:
El retículo de los divisores de N es complementado si y sólo si N es libre de cuadrados.
En efecto: Si N es libre de cuadrados, todos sus factores primos estarán elevados a la unidad, por lo que cada divisor a se caracterizará tan sólo por su colección de factores primos, y bastará tomar para a’ el número formado por el producto de los primos que no son divisores de a, que cumplirá trivialmente lo exigido. Por ejemplo, entre los divisores de 210 (libre de cuadrados porque 210=2*3*5*7), el complemento de 35 es 14.
Por el contrario, si no es libre de cuadrados, un divisor al menos p se presenta elevado a una potencia con exponente r mayor que 1. Busquemos el complemento q de p (sin elevar a r). En primer lugar deberá cumplir que pÙq=F o expresado mejor en este caso, p y q han de ser coprimos. Entonces q sólo podrá contener factores primos distintos de p. Pero al calcular pÚq el resultado no podrá coincidir con N, ya que el MCM(p, q) contendrá a p elevado a la unidad, mientras que N lo contiene elevado a r>1. Así que ningún candidato a complemento cumple las dos propiedades. Hemos encontrado un contraejemplo que invalida la propiedad.
Este carácter de retículo se suele expresar mediante un diagrama de Hasse, en el que cada dos elementos relacionados se unen mediante una línea, no teniendo en cuenta la propiedad reflexiva y aprovechando la transitiva para eliminar líneas. Aquí tienes el correspondiente a 150:
Se comprende que hay otras formas de ordenarlo y dibujarlo. Es un buen ejercicio identificar el carácter de un número según su diagrama de divisores (potencia de un primo, semiprimo, libre de cuadrados…)
Presentada esquemáticamente la teoría, nos dedicaremos a descubrir algunos retículos y semirretículos que se dan en el conjunto de divisores de N. Todo él completo hemos visto que es un retículo.
Pero eso queda para otro día
lunes, 13 de mayo de 2013
Particiones con sumandos restringidos
En la anterior entrada hemos supuesto que el número de sumandos en una partición era libre, hasta el mayor posible. Puede ocurrir, sin embargo, que sólo deseemos usar un máximo de hasta tres sumandos, o exactamente cuatro o cualquier otra posibilidad. Por otra parte, los sumandos pueden estar restringidos en magnitud dentro de un rango. Esto complica un poco las cuestiones.
Veremos con algunos ejemplos la utilidad de las funciones generatrices y la posibilidad de comprobar resultados con la hoja Cartesius.
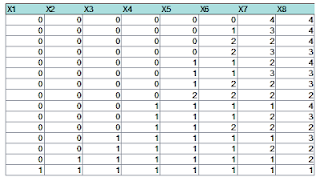
¿De cuántas formas se puede descomponer el número 8 en sumandos no mayores que 4?
Si has entendido de qué van las funciones generatrices comprobarás que la siguiente es la adecuada para este caso
Como en casos anteriores podemos expresarlo como sumas de sucesiones geométricas
Y en general
Para aplicarlo al caso de 8 bastará buscar su coeficiente en la F.G. aplicada al caso en el que k=4. Lo escribimos en PARI
print(taylor(1/(1-x)/(1-x^2)/(1-x^3)/(1-x^4),x,9))
Y obtenemos
F.G.=1+x+2x^2+3*x^3+5*x^4+6*x^5+9*x^6+11*x^7+15*x^8+O(x^9)
Luego la solución del problema es P(8/sumandos no mayores que 4)=15
Si lo planteamos con Cartesius obtenemos los 15
Particiones conjugadas
Ahora usaremos una técnica muy simple, pero que da buenos resultados. Como veíamos en otra entrada (http://hojaynumeros.blogspot.com.es/2011/02/particiones-de-un-numero.html) cada una de las particiones se puede representar mediante un diagrama de Ferrer, en el que se adosan tantas filas como sumandos entran en la partición, siendo la longitud de cada columna el valor del sumando. Así, la partición 8=4+2+1+1 se puede representar como
Cada fila representa un sumando: 4, 2, 1 y 1. Todos los diagramas que formemos con estas 15 particiones tendrán como máxima anchura cuatro cuadrados.
Lo bueno de estos diagramas, entre otras ventajas, es que si los giramos convirtiendo las filas en columnas y las columnas por filas seguirán siendo particiones, llamadas particiones conjugadas.
Así, la partición 3+2+1+1+1
Se puede convertir en 5+2+1
Esta correspondencia es biyectiva. Si en las 15 particiones consideradas ninguna podía sobrepasar la anchura de 4, sus conjugadas no podrán tener más de cuatro filas, es decir, más de cuatro sumandos.
Esto es muy interesante: Las particiones en sumandos no mayores que k coinciden en número con las particiones en no más de k sumandos.
En nuestro ejemplo: si existen 15 particiones de 8 en sumandos no mayores que 4, también serán 15 las que se obtengan con no más de cuatro sumandos libres.
Lo comprobamos, intercambiando en Cartesius el 4 con el 8, y vemos que resultan también 15:
Así que si alguna vez no puedes construir la F.G. de un tipo de particiones, puedes acudir a las conjugadas por si resulta más sencillo. El siguiente ejemplo lo aclara.
¿De cuántas formas distintas podemos descomponer el número 12 en exactamente cuatro sumandos?
Acudimos a la conjugada: Este problema es el mismo que descomponer 12 en sumas de las cuales el mayor sumando sea 4. De otra forma: debe figurar al menos un 4 y el resto ser 1,2 o 3.
De esa forma la F.G. es fácil de obtener:
(hemos suprimido el 1 en el mayor sumando)
Generalizando
Efectuamos las comprobaciones en nuestro ejemplo
Con la función generatriz y PARI
print(taylor(x^4/(1-x)/(1-x^2)/(1-x^3)/(1-x^4),x,9))
Desarrollo: x^4+x^5+2*x^6+3*x^7+5*x^8+6*x^9+9*x^10+11*x^11+15*x^12+O(x^13)
Solución: el coeficiente de 12, que es 15.
Con Cartesius
Tenemos que eliminar el cero de los sumandos, para que sean exactamente cuatro. Por eso el rango será 1..12
Resultado: 15
Problema conjugado
Ahora, en lugar de cuatro sumandos, el máximo ha de ser siempre 4, pero eso no es operativo, pues podemos eliminar siempre ese 4 y en lugar de formar una suma 12 pedimos que la suma sea 8. Este problema lo tenemos resuelto más arriba y nos resultó 15, como era de esperar.
lunes, 6 de mayo de 2013
Particiones y funciones generatrices
Unimos hoy dos conceptos que ya hemos tratado en el blog
http://hojaynumeros.blogspot.com.es/2011/01/montones-de-piezas.html y siguientes
http://hojaynumeros.blogspot.com.es/2013/03/funciones-generatrices-en-combinatoria.html y siguiente.
y que al unirse dan resultados mucho más potentes. Recomendamos la lectura previa de ambas. Recorreremos ahora los principales tipos de particiones, ayudados también por nuestra hoja de cálculo Cartesius.
Particiones ordinarias P(n)
En la entrada ya referida las estudiamos desde un punto de vista general. Aplicaremos ahora el concepto de función generatriz.
Supongamos que deseamos encontrar todas las particiones ordinarias del número 6 (formas de representar 6 como suma con posible repetición de sumandos). Para ello no necesitamos ni funciones ni técnicas informáticas. Con un poco de atención llegaremos a que el 6 se descompone en suma de las siguientes formas:
6 = 5+1 = 4+2 = 4+1+1 = 3+3 = 3+2+1 = 3+1+1+1 = 2+2+2 = 2+2+1+1 = 2+1+1+1+1 = 1+1+1+1+1+1
Son once en total
Si queremos expresar este proceso mediante funciones generatrices hay que recordar que los sumandos provenían de exponentes en un polinomio. En efecto, en este caso del 6 podemos considerar la función
O expresado de forma sintética y generalizando hasta n:
Después volveremos a esta función generatriz para adaptarla a casos particulares. La comprobamos para n=6. Vimos en anteriores entradas que con PARI se pueden desarrollar fácilmente.
print(taylor(1/(1-x)/(1-x^2)/(1-x^3)/(1-x^4)/(1-x^5)/(1-x^6),x,7))
Resultado: 1+x+2x^2+3x^3+5x^4+7x^5+11x^6+O(x^7) con el coeficiente 11 para x^6, como era de esperar. Serían las once particiones esperadas. Como en ocasiones anteriores, este método nos da más, pues podemos leer otros coeficientes: con el 5 tendríamos 7 particiones, con el 4, 5, y así…A la inversa, si en lugar de pararnos en el 6 hubiéramos seguido escribiendo factores, obtendríamos más particiones, para 7, 8,… Así que recordemos la función generatriz (F.G.) para las particiones ordinarias del número n:
Podemos comprobar el resultado con nuestra hoja Cartesius. Basta programar esto:
Concreta un total de 6 conjuntos, formado cada uno por el rango 0..6, en el que sólo se seleccionan los arreglos crecientes (para evitar duplicidades) y con suma 6.
Obtendríamos once resultados
Intenta obtener otros resultados similares. Lo importante es que recuerdes la definición de partición de un número y su F.G.
Particiones en sumandos distintos Q(N)
Si al descomponer un número en sumandos no permitimos que figuren repetidos, obtendríamos resultados muy distintos, recogidos como la función de partición Q(n).
En este caso la función generatriz se simplifica mucho, pues en los paréntesis no han de figurar todas las potencias sino una sola por cada sumando. Así, para n=7 la F.G. sería
y generalizando para n
Para el caso de 7 podemos expandir la F.G. mediante wxMaxima
Obtendremos un desarrollo en forma de polinomio, pero sólo serán útiles los coeficientes menores o iguales a 7:
Ya tenemos la solución, el 7 se puede descomponer en 5 formas diferentes como suma de números naturales distintos:
7=6+1=5+2=4+3=4+2+1
Además, hemos obtenido que el 6 tiene 4 descomposiciones, el 5, 3 y así hasta el 1. Recuerda: estos son los únicos fiables en el desarrollo.
Con Cartesius:
5 soluciones
Particiones en partes impares P(N/Impar)
Aquí vemos rápidamente la utilidad de la función generatriz. Si en la fórmula general de las particiones eliminamos los pares de los paréntesis quedaría
que fácilmente se traduce, al igual que en las particiones ordinarias, a cocientes:
O bien
Por ejemplo, para n=7, usando PARI, nos resultaría
print(taylor(1/(1-x)/(1-x^3)/(1-x^5)/(1-x^7),x,8))
1+x+x^2+2*x^3+2*x^4+3*x^5+4*x^6+5*x^7+O(x^8)
Como el coeficiente de 7 es 5, ese será el número de particiones en impares. Como son tan pocas, las podemos escribir directamente: 7 = 5+1+1 = 3+3+1 = 3+1+1+1+1 = 1+1+1+1+1+1+1
Intenta comprobar, como en los casos anteriores, que con 6 resultarían 4, con 5, 3, y así con todos los coeficientes resultantes.
Comprobación con Cartesius
La instrucción CONCERO significa que a los impares les adjuntamos el cero para representar los sumandos que no entran en una suma determinada. Además, se impone la condición de ser impares.
5 soluciones:
Este resultado coincide con el de representar 7 con sumandos distintos. En realidad siempre es así, como demostró Euler usando funciones generatrices:
El número de particiones de un número en sumandos distintos coincide con el de particiones en sumandos impares
Con el uso de las F.G. todo se reduce a un artificio algebraico:
Demostración
Todo se basa en que
Así que partiendo de la F.G. de la partición en elementos distintos, representamos cada factor de esta forma, se simplificarán los factores de exponente par y sólo quedarán los impares en el denominador
En el caso de n=7 te proponemos una correspondencia biyectiva por el método de Sylvester. Para que pienses un poco más sólo daremos el proceso y tú sacas tus consecuencias:
7=6+1=5+2=4+3=4+2+1 = 2*3+1 = 5+2*1=4*1+3=4*1+2*1+1 y ahora sustituimos cada producto por la suma correspondiente: 7 = 3+3+1 = 5+1+1 = 1+1+1+1+3 = 1+1+1+1+1+1+1
¿Puedes generalizarlo?
Para el camino inverso deberíamos expresar cada suma de repetidos como suma respecto a potencias de 2 distintas que se sacan como factor común.
7 = 3+3+1 = 5+1+1 = 1+1+1+1+3 = 1+1+1+1+1+1+1 = 3*2+1=5+2*1=4*1+3=4*1+2*1+1
Serían siempre todos distintos, porque o se diferencian en el números sacado factor común o en las distintas potencias de 2
Suscribirse a:
Entradas (Atom)