Sumas del tipo m+n+mn

Como en otras ocasiones, cualquier comentario o reto aparecido en las redes sociales nos sirve de excusa para emprender un estudio. Hoy nos dedicaremos al número de descomposiciones del tipo k=m+n+mn (m>0 y n>0) que puede presentar un número k. A efectos prácticos podemos suponer que n es mayor o igual a m.

El número 99, por ejemplo, admite cuatro descomposiciones:

99=3+24+3*24
99=4+19+4*19
99=9+9+9*9
99=1+49+1*49

Otros números tan populares como el 30 no admiten ninguna descomposición de este tipo.

¿De cuántas formas se puede descomponer un número determinado? Como en ocasiones similares, comenzaremos con procedimientos de “fuerza bruta”, para ir después refinando el estudio hasta llegar al planteamiento teórico.

Con el Basic de Excel y Calc

En primer lugar debemos considerar que el valor mínimo para m y n es 1, luego el valor máximo será:

Si k=m+n+mn y damos a m el valor 1, despejando n resulta:

K=1+n+n, luego n<=(k-1)/2 y este valor sería la cota para m y n. Por otra parte, al despejar n en general, n=(k-m)/(m+1), este valor ha de ser entero y mayor que m (si queremos evitar repeticiones). Con esto ya podemos construir un algoritmo para contar el número de descomposiciones de este tipo que presenta un número dado.

Public Function numsumamn(k)
Dim m, n,  p

p = 0 ‘Contador de éxitos
For m = 1 To (k - 1) / 2 ‘m recorre el rango desde 1 hasta la cota
n = (k - m) / (m + 1) ‘El valor de n se despeja respecto a m
If n >= m And n = Int(n) Then p = p + 1 ‘Si es entero y mayor o igual a m, vale
Next m
numsumamn = p
End Function

Con este algoritmo podemos confeccionar tablas para esta función. La siguiente corresponde a los 20 primeros números:

Vemos que, por ejemplo, el 15 debe descomponerse de dos formas. Aquí las tienes:

1+7+1*7=15; 3+3+3*3=15

Algoritmo con el lenguaje PARI

Este algoritmo se traduce con facilidad al lenguaje PARI:

numsumamn(k)=local(p=0);for(m=1,(k-1)/2,n=(k-m)/(m+1);if(n==truncate(n)&&n>=m,p+=1));p

Con él y una estructura repetitiva puedes encontrar un listado de enteros con un número de descomposiciones fijado. El siguiente código nos devuelve los primeros números que admiten tres descomposiciones:

numsumamn(k)=local(p=0);for(m=1,(k-1)/2,n=(k-m)/(m+1);if(n==truncate(n)&&n>=m,p+=1));p
for(i=1,200,if(numsumamn(i)==3,print1(i,", ")))

Veamos el caso del 55: 1+27+1*27=3+13+3*13=7+6+7*6=55

Se obtienen las tres descomposiciones previstas.

Puedes experimentar con estos algoritmos, aunque al final de la entrada aprenderás un método mucho más eficiente.

Comprobación con Cartesius

Nuestra hoja de cálculo Cartesius (http://www.hojamat.es/sindecimales/combinatoria/herramientas/herrcomb.htm#cartesius),que desarrolla productos cartesianos condicionados, nos puede servir para comprobar los valores de la función numsumamn. Como sabemos que la cota para m y n es (k-1)/2, (o k/2 para simplificar), bastará combinar los distintos valores de ambos y destacar tan solo aquellos en los que m+n+mn=k. Quedaría así en el caso de k=71:

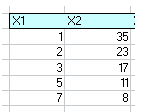
En primer lugar se fijan 2 elementos (serían m y n). Después se hacen recorrer el rango 1..36, que es la cota aproximada por exceso. La parte importante es la de exigir es x1+x2+x1*x2=71, según la cuestión que estamos resolviendo, y, por último, pedimos arreglos crecientes para eliminar duplicidades. Nos deberían dar 5 soluciones, según el valor de numsumamn(71), y, en efecto, los resultados son:

Lo podemos calcular: 1+35+1*35=36+35=71; 2+23+2*23=25+46=71; 3+17+3*17=20+51=71;
5+11+5*11=16+55=71; 7+8+7*8=15+56=71.

Puedes comprobar así cualquier valor de numsumamn(k)

Estudio teórico

Todo lo anterior se basa en un estudio “ingenuo”, en el que no se analiza la cuestión y sólo se pretende obtener resultados. Ahora veremos que los mismos tienen un fundamento teórico muy simple, que nos llevará a una fórmula para el número de descomposiciones del tipo m+n+mn=k

Basta darse cuenta de que la expresión estudiada equivale a (m+1)(n+1)-1. Por ejemplo, 2+35+2*35=37+70=107 es igual a (2+1)(35+1)-1=3*36-1=108-1=107.

Esto nos aclara la situación, porque el número de descomposiciones del tipo m+n+mn para un número k coincide con el de los pares de divisores cuyo producto es k+1. Así, las cuatro descomposiciones del número 99 (3+24+3*24, 4+19+4*19, 9+9+9*9, 1+49+1*49) coinciden con todos los pares de divisores (m+1)(n+1) del número k+1, en este caso 100. En efecto, los pares son: 2*50, que da lugar a 1+49+1*49, 4*25, que produce 3+24+3*24, 5*20 para 4+19+4*19 y 10*10, que se empareja con 9+9+9*9

El número de descomposiciones de k en expresiones m+n+mn coincide con el del número de pares de productos p*q=k+1 con p>1 y q>1.

El número de pares de este tipo está relacionado con la función TAU de k+1, que cuenta el número de divisores que posee k+1, y que tiene la expresión

En ella los valores de a₁, a₂,, a₃,,…son los exponentes de los factores primos de k+1. Si el valor de esa función es par, el número de productos p*q=k+1 será la mitad, y si es impar, la mitad más 1. A ese resultado habrá que restarle 1, porque el par 1*(k+1) no nos sirve. Así que quedaría:

Podemos comprobarlo con ejemplos concretos:

K=23; 24=2³*3; TAU(24)=(1+3)(1+1)=8; 8/2-1=3. Los pares válidos de divisores serán 2*12, 3*8, 4*6. Así que 23 debe admitir tres descomposiciones. Es fácil ver que son estas: 1+11+1*11, 2+7+2*7 y 3+5+3*5. Aquí tienes la comprobación con Cartesius:

En el caso de k+1=144, cuadrado perfecto, su función TAU es impar, lo que da sentido al hecho de que usemos la parte entera. Lo vemos:

K=143; k+1=144; 144=2⁴*3²; TAU(144)=(1+4)(1+2)=15; INT((15+1)/2)=8; 8-1=7.

Deberán aparecer 7 soluciones para los productos de divisores:2*72, 3*48, 4*36, 6*24, 8*18, 9*16, 12*12. Existirán, pues, 7 soluciones para nuestro problema. Las conseguimos con Cartesius:

Puedes irlas comprobando: 1+71+1*71=72+71=143; 2+47+2*47=49+94=143,…

Casos particulares

K+1 primo

Según lo anterior, los valores de k tales que k+1 sea primo, no admitirán la descomposición en m+n+mn.

Recuerda que entre los primeros 20 números tenemos (ver tabla de arriba) que 1, 2, 4, 6, 10, 12, 16, y 18 no admiten descomposiciones m+n+mn. Súmales una unidad y te resultarán los primeros primos: 2, 3, 5, 7, 11, 13,…

K+1 semiprimo

Los semiprimos poseen sólo dos factores primos, luego en ellos TAU=(1+1)(1+1)=4, y como 4/2-1=1, resultará que k sólo admitirá una descomposición. Es el caso de 3, 5, 8, 9,…en los que k+1 es semiprimo: 4=2*2, 6=2*3, 9=3*3, 10=2*5.

La propiedad contraria no es cierta, ya que 7 sólo admite la descomposición 1+3+1*3 y 8 no es semiprimo.

K+1 cuadrado

Si k+1 es cuadrado, k presentará una suma en la que m=n, como es fácil ver. Si k+1=p*p, k será igual a p-1+p-1+(p-1)(p-1). Es el caso, por ejemplo de 48, ya que 49=7*7 y 48=6+6+6*6.

Lo dejamos aquí. Este tipo de cuestiones elementales que dan lugar a experimentaciones sencillas se pueden abordar en las clases de Matemáticas de la Enseñanza Media. Sería divertido lanzar la idea en un trabajo por grupos y ver cada uno qué caminos emprende en sus búsquedas. No sería extraño que alguno diera con el truco del k+1.